fastmath.optimization

Optimization.

Namespace provides various optimization methods.

Brent (1d functions)
Bobyqa (2d+ functions)
Powell
Nelder-Mead
Multidirectional simplex
CMAES
Gradient
Bayesian Optimization (see below)

All optimizers require bounds.

Optimizers

To optimize functions call one of the following functions:

minimize or maximize - to perform actual optimization
scan-and-minimize or scan-and-maximize - functions find initial point using brute force and then perform optimization paralelly for best initialization points. Brute force scan is done using jitter low discrepancy sequence generator.

You can also create optimizer (function which performs optimization) by calling minimizer or maximizer. Optimizer accepts initial point.

All above accept:

one of the optimization method, ie: :brent, :bobyqa, :nelder-mead, :multidirectional-simplex, :cmaes, :gradient
function to optimize
parameters as a map

For parameters meaning refer Optim package

Common parameters

:bounds (obligatory) - search ranges for each dimensions as a seqence of [low high] pairs
:initial - initial point other then mid of the bounds as vector
:max-evals - maximum number of function evaluations
:max-iters - maximum number of algorithm interations
:bounded? - should optimizer force to keep search within bounds (some algorithms go outside desired ranges)
:stats? - return number of iterations and evaluations along with result
:rel and :abs - relative and absolute accepted errors

For scan-and-... functions additionally you can provide:

:N - number of brute force iterations
:n - fraction of N which are used as initial points to parallel optimization
:jitter - jitter factor for sequence generator (for scanning domain)

Specific parameters

BOBYQA - :number-of-points, :initial-radius, :stopping-radius
Nelder-Mead - :rho, :khi, :gamma, :sigma, :side-length
Multidirectional simples - :khi, :gamma, :side-length
CMAES - :check-feasable-count, :diagonal-only, :stop-fitness, :active-cma?, :population-size
Gradient - :bracketing-range, :formula (:polak-ribiere or :fletcher-reeves), :gradient-h (finite differentiation step, default: 0.01)

Bayesian Optimization

Bayesian optimizer can be used for optimizing expensive to evaluate black box functions. Refer this article or this article

bayesian-optimization

(bayesian-optimization f {:keys [warm-up init-points bounds utility-function-type utility-param kernel kscale jitter noise optimizer optimizer-params normalize?], :or {kscale 1.0, kernel (k/kernel :mattern-52), warm-up (* (count bounds) 1000), init-points 3, utility-function-type :ucb, utility-param (if (#{:ei :poi} utility-function-type) 0.001 2.576), jitter 0.25, normalize? true}})

Bayesian optimizer

Parameters are:

:warm-up - number of brute force iterations to find maximum of utility function
:init-points - number of initial evaluation before bayesian optimization starts. Points are selected using jittered low discrepancy sequence generator (see: jittered-sequence-generator
:bounds - bounds for each dimension
:utility-function-type - one of :ei, :poi or :ucb
:utility-param - parameter for utility function (kappa for ucb and xi for ei and poi)
:kernel - kernel, default :mattern-52, see fastmath.kernel
:kscale - scaling factor for kernel
:jitter - jitter factor for sequence generator (used to find initial points)
:noise - noise (lambda) factor for gaussian process
:optimizer - name of optimizer (used to optimized utility function)
:optimizer-params - optional parameters for optimizer
:normalize? - normalize data in gaussian process?

Returns lazy sequence with consecutive executions. Each step consist:

:x - maximum x
:y - value
:xs - list of all visited x’s
:ys - list of values for every visited x
:gp - current gaussian process regression instance
:util-fn - current utility function
:util-best - best x in utility function

Examples

Usage

(let [bounds [[-5.0 5.0] [-5.0 5.0]]
      f (fn [x y]
          (+ (m/sq (+ (* x x) y -11.0)) (m/sq (+ x (* y y) -7.0))))]
  (nth (bayesian-optimization
        (fn [x y] (- (f x y)))
        {:bounds bounds, :init-points 5, :utility-function-type :poi})
       10))
;;=> {:gp
;;=>  #object[fastmath.regression$gaussian_process_PLUS_$reify__21681 0x59e1b2e4 "fastmath.regression$gaussian_process_PLUS_$reify__21681@59e1b2e4"],
;;=>  :util-best (3.5903573476155994 -1.3047510850380841),
;;=>  :util-fn #,
;;=>  :x (3.6110565699304544 -1.940965611119334),
;;=>  :xs ((3.5903573476155994 -1.3047510850380841)
;;=>       (3.5247794796446748 -1.6451582982884116)
;;=>       (3.6789786986648707 -1.7530716713395997)
;;=>       (3.4577121536528175 -1.8547818785182897)
;;=>       (3.613388143239664 -1.9728663702896228)
;;=>       (3.6451089036425888 -1.9540854072228746)
;;=>       (3.6110565699304544 -1.940965611119334)
;;=>       (3.4688634898961865 -2.106216937383449)
;;=>       (3.376189955128096 -2.266979120530924)
;;=>       (3.386970650418002 -2.4325266303298863)
;;=>       (2.880695310551139 -2.9146299798030673)
;;=>       [-1.156162110864245 -2.9468958540653127]
;;=>       [-4.2146503347211794 2.048293179286917]
;;=>       [2.9490730720706617 -2.8382122273977033]
;;=>       [0.5880514819443707 2.845054307229818]
;;=>       [-1.9815897641665918 -1.2801470348071868]),
;;=>  :y -0.15294395869271743,
;;=>  :ys (-3.2580576430126014
;;=>       -0.6397406526436549
;;=>       -0.672616453253476
;;=>       -0.8186350559903253
;;=>       -0.26262805090280883
;;=>       -0.3255982421303834
;;=>       -0.15294395869271743
;;=>       -1.9708137666300416
;;=>       -5.787011058930222
;;=>       -9.154487154927054
;;=>       -50.68928156200132
;;=>       -159.2955853434706
;;=>       -126.91217880409326
;;=>       -42.467928495377635
;;=>       -63.81310640644723
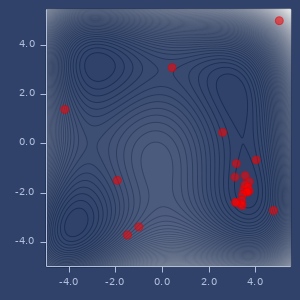
;;=>       -123.69701853631281)}

Bayesian optimization points

view source

maximize

(maximize method f config)

Maximize given function.

Parameters: optimization method, function and configuration.

Examples

Usage

(let [bounds [[-5.0 5.0]]
      f (fn [x]
          (+ (* 0.2 (m/sin (* 10.0 x)))
             (/ (+ 6.0 (- (* x x) (* 5.0 x))) (inc (* x x)))))]
  {:powell (maximize :powell f {:bounds bounds}),
   :brent (maximize :brent f {:bounds bounds})})
;;=> {:brent [(-0.4523106823170646) 7.224689671203529],
;;=>  :powell [(-0.4522927913307559) 7.224689666542709]}

view source

maximizer

(maximizer method f config)

Create optimizer which maximizer function.

Returns function which performs optimization for optionally given initial point.

Examples

Usage

(let [bounds [[-5.0 5.0]]
      f (fn [x]
          (+ (* 0.2 (m/sin (* 10.0 x)))
             (/ (+ 6.0 (- (* x x) (* 5.0 x))) (inc (* x x)))))
      optimizer (maximizer :cmaes f {:bounds bounds})]
  {:optimizer optimizer,
   :run-1 (optimizer),
   :run-2 (optimizer [4.5]),
   :run-3 (optimizer [-4.5])})
;;=> {:optimizer #,
;;=>  :run-1 [(0.0) 6.0],
;;=>  :run-2 [(-0.638637412113197) 6.799011722273228],
;;=>  :run-3 [(-1.3504713306913132) 5.0006182942218445]}

view source

minimize

(minimize method f config)

Minimize given function.

Parameters: optimization method, function and configuration.

Examples

1d function

(let [bounds [[-5.0 5.0]]
      f (fn [x]
          (+ (* 0.2 (m/sin (* 10.0 x)))
             (/ (+ 6.0 (- (* x x) (* 5.0 x))) (inc (* x x)))))]
  {:powell (minimize :powell f {:bounds bounds}),
   :brent (minimize :brent f {:bounds bounds}),
   :brent-with-initial-point
   (minimize :brent f {:bounds bounds, :initial [2.0]})})
;;=> {:brent [(-3.947569586073323) 2.2959519482739297],
;;=>  :brent-with-initial-point [(2.979593427579756) -0.20178173314322778],
;;=>  :powell [(2.3572022329682807) -0.23501046849989368]}

2d function

(let [bounds [[-5.0 5.0] [-5.0 5.0]]
      f (fn [x y]
          (+ (m/sq (+ (* x x) y -11.0)) (m/sq (+ x (* y y) -7.0))))]
  {:bobyqa (minimize :bobyqa f {:bounds bounds}),
   :gradient (minimize :gradient f {:bounds bounds})})
;;=> {:bobyqa [(3.5844283403693833 -1.848126526921083)
;;=>           1.1846390625694734E-19],
;;=>  :gradient [(2.999999285787787 2.0000014646814326)
;;=>             3.442177688274934E-11]}

With stats

(minimize :gradient
          (fn* [p1__21909#] (m/sin p1__21909#))
          {:bounds [[-5 5]], :stats? true})
;;=> {:evaluations 22, :iterations 3, :result [(-1.5707963273649799) -1.0]}

min/max of f using :powell optimizer

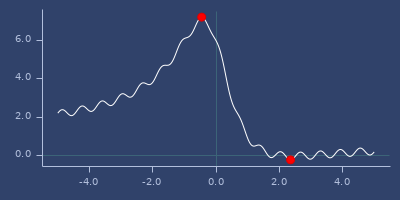
min/max of f using :nelder-mead optimizer

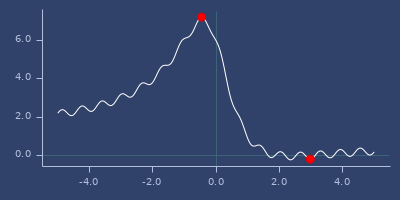
min/max of f using :multidirectional-simplex optimizer

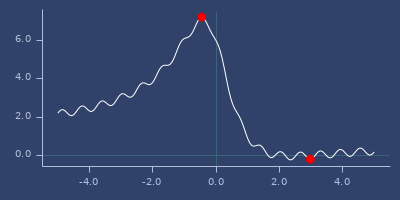
min/max of f using :cmaes optimizer

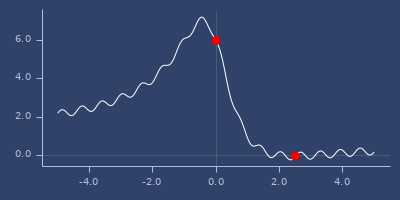
min/max of f using :gradient optimizer

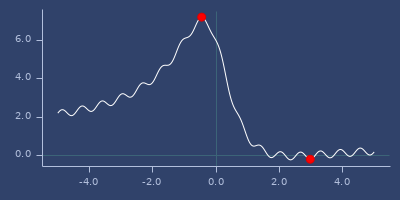
min/max of f using :brent optimizer

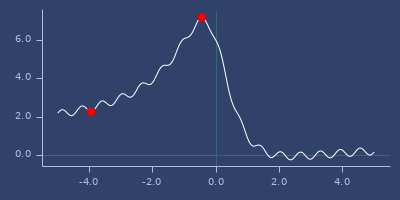
min/max of f using :powell optimizer

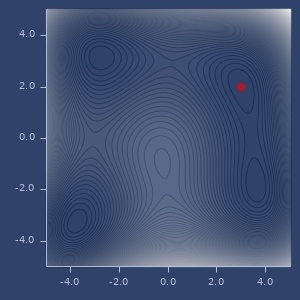
min/max of f using :nelder-mead optimizer

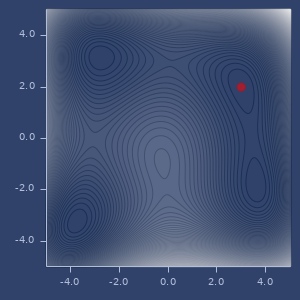
min/max of f using :multidirectional-simplex optimizer

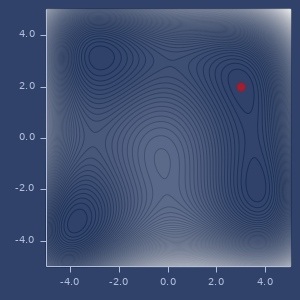
min/max of f using :cmaes optimizer

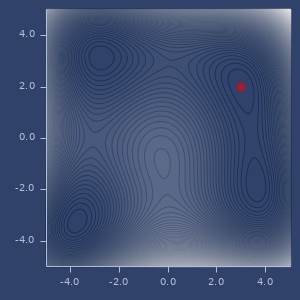
min/max of f using :gradient optimizer

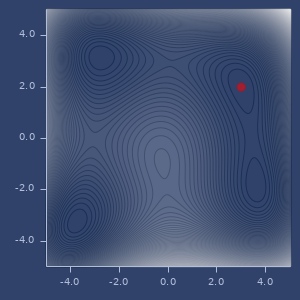
min/max of f using :bobyqa optimizer

view source

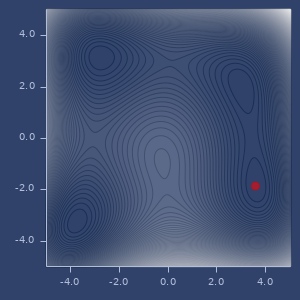
minimizer

(minimizer method f config)

Create optimizer which minimizes function.

Returns function which performs optimization for optionally given initial point.

Examples

Usage

(let [bounds [[-5.0 5.0]]
      f (fn [x]
          (+ (* 0.2 (m/sin (* 10.0 x)))
             (/ (+ 6.0 (- (* x x) (* 5.0 x))) (inc (* x x)))))
      optimizer (minimizer :brent f {:bounds bounds})]
  {:optimizer optimizer,
   :run-1 (optimizer),
   :run-2 (optimizer [4.5]),
   :run-3 (optimizer [-4.5])})
;;=> {:optimizer #,
;;=>  :run-1 [(-3.947569586073323) 2.2959519482739297],
;;=>  :run-2 [(2.357114991599655) -0.2350104692683484],
;;=>  :run-3 [(-4.570514545168775) 2.074718566761628]}

view source

scan-and-maximize

Examples

Usage

(let [bounds [[-5.0 5.0]]
      f (fn [x]
          (+ (* 0.2 (m/sin (* 10.0 x)))
             (/ (+ 6.0 (- (* x x) (* 5.0 x))) (inc (* x x)))))]
  {:powell (scan-and-maximize :powell f {:bounds bounds}),
   :brent (scan-and-maximize :brent f {:bounds bounds})})
;;=> {:brent [(-0.45231069920367) 7.22468967120353],
;;=>  :powell [(-0.4523086554997955) 7.224689671143135]}

view source

scan-and-minimize

Examples

1d function

(let [bounds [[-5.0 5.0]]
      f (fn [x]
          (+ (* 0.2 (m/sin (* 10.0 x)))
             (/ (+ 6.0 (- (* x x) (* 5.0 x))) (inc (* x x)))))]
  {:powell (scan-and-minimize :powell f {:bounds bounds}),
   :brent (scan-and-minimize :brent f {:bounds bounds})})
;;=> {:brent [(2.3571149062671237) -0.23501046926842564],
;;=>  :powell [(2.3566677130060376) -0.23501046925872443]}

2d function

(let [bounds [[-5.0 5.0] [-5.0 5.0]]
      f (fn [x y]
          (+ (m/sq (+ (* x x) y -11.0)) (m/sq (+ x (* y y) -7.0))))]
  {:bobyqa (scan-and-minimize :bobyqa f {:bounds bounds}),
   :gradient (scan-and-minimize :gradient f {:bounds bounds})})
;;=> {:bobyqa [(2.9999999999935567 2.000000000056682)
;;=>           4.8850752449334874E-20],
;;=>  :gradient [(3.5844284040527805 -1.8481254141694856)
;;=>             1.886170811455982E-11]}

view source

Generated by Codox with RDash UI theme

Fastmath 1.5.3-SNAPSHOT

Project

Namespaces

Public Vars

fastmath.optimization

Optimizers

Common parameters

Specific parameters

Bayesian Optimization

Categories

bayesian-optimization

Examples

maximize

Examples

maximizer

Examples

minimize

Examples

minimizer

Examples

scan-and-maximize

Examples

scan-and-minimize

Examples