fastmath.kernel
Various kernel functions.
- RBF (double -> double functions)
- vector kernels (vector x vector -> double function; may be positive definite, conditional positive definite, positive semi-definite, mercer)
- density estimation
- some kernel operations
Categories
Other vars: approx cauchy-density-kernel cosine-density-kernel cpd->pd epanechnikov-density-kernel exp fields gaussian-density-kernel kernel kernel->rbf kernel-density kernel-density-ci kernel-density-list kernels-list laplace-density-kernel logistic-density-kernel mult quartic-density-kernel rbf rbf->kernel rbf-list scale sigmoid-density-kernel silverman-density-kernel smile-mercer smile-rbf triangular-density-kernel tricube-density-kernel triweight-density-kernel uniform-density-kernel wadd wigner-density-kernel
approx
(approx k precision)(approx k)Kernel wrapper. Round value returned by kernel using fastmath.core/approx function.
Examples
Usage
(let [ak (approx (kernel :gaussian))] (ak [1 2] [3 4]))
;;=> 0.02
(let [ak (approx (kernel :gaussian) 6)] (ak [1 2] [3 4]))
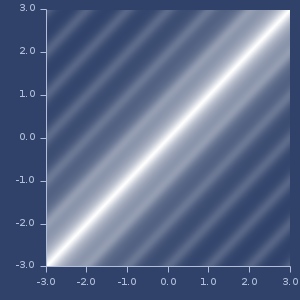
;;=> 0.018316Plot of
:gaussiankernel pproximated to one decimal place.
cpd->pd
(cpd->pd k)Convert conditionally positive definite kernel into positive definite.
Formula is based on this SO answer. x0 is equal 0.
Doesn’t work well.
Examples
Usage
(let [k (kernel :circular) pd (cpd->pd k)] (pd [0.0 -0.1] [0.2 0.4]))
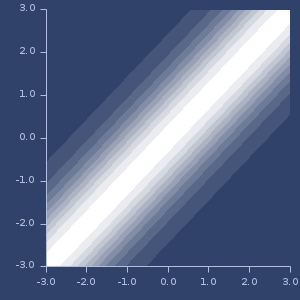
;;=> 0.013011305Plot of
:periodickernel converted withcpd->pdfunction.
exp
(exp k)(exp k t)Kernel wraper. exp of kernel k with optional scaling value t.
Examples
Usage
(let [k (exp (kernel :laplacian))] (k [1 2] [3 4]))
;;=> 1.060887420006057Exp with scale=0.5
(let [k (exp (kernel :laplacian) 0.5)] (k [1 2] [3 4]))
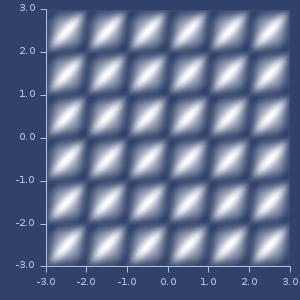
;;=> 1.0299938931887205Plot of exp of
:dirichletkernel with scaling=5.0
fields
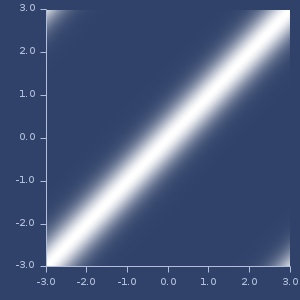
(fields k f)(fields k f1 f2)Kernel wrapper. Apply vector field for each input before applying kernel function.
Examples
Usage
(let [k (kernel :laplacian)
fld (fields/field :horseshoe)
kf (fields k fld)]
(kf (v/vec2 2 3) (v/vec2 1 2)))
;;=> 0.21437946979352915kernel
multimethod
Crated vector kernel.
Kernels can be Mercer, positive definite, conditional positive definite, positive semi-definite or other.
Optional parameters:
For :gaussian, :exponential, :laplacian, :rational-quadratic, :multiquadratic, :inverse-multiquadratic, :circular, :spherical, :wave, :power, :log, :cauchy, :generalized-t-student, :hyperbolic-secant, :thin-plate, :mattern-12, :mattern-32, :mattern-52 and ::hyperbolic-secant you can provide scaling parameter and distance (see fastmath.distance, default is euclidean).
Others:
:linear-alpha, scaling parameter:polynomial-alpha(scaling),c(shift) andd(power):anova-sigma(scaling),kandd(power):hyperbolic-tangent-alpha(scaling),c(shift):periodic-sigma(scaling),periodicityanddistance:bessel-sigma(scaling),nandv(power factors) anddistance:generalized-histogram-alphaandbeta(power factors):dirichlet-N:pearson-sigma(scaling) andomega(power)
Additionally there are two special kernels build from funcitons:
:scalar-functions- provide one or two double->double functions:variance-function- provide any variance function (smooth, vector->double type)
The rest of the kernels do not require parameters.
Examples
Usage
(let [k (kernel :gaussian)] (k [1 2 3 4] [-1 2 3 5]))
;;=> 0.08208499862389877
(let [k (kernel :gaussian 1.0 d/chebyshev)] (k [1 2 3 4] [-1 2 3 5]))
;;=> 0.1353352832366127
(let [k (kernel :thin-plate)] (k [1 2 3 4] [-1 2 3 5]))
;;=> 4.023594781085252
(let [k (kernel :mattern-52 0.5)] (k [1 2 3 4] [-1 2 3 5]))
;;=> 0.0020127302194701585Plot of anova
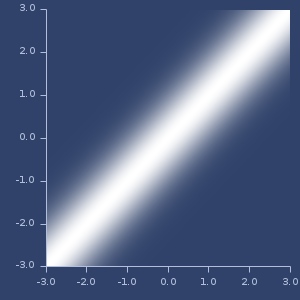
Plot of bessel
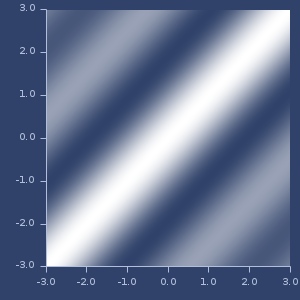
Plot of cauchy
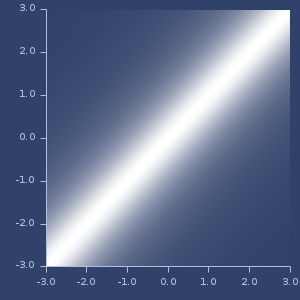
Plot of chi-square-cpd
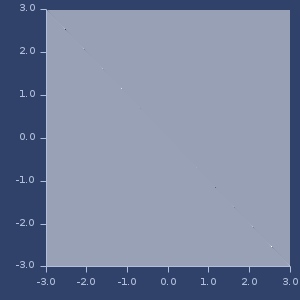
Plot of chi-square-pd
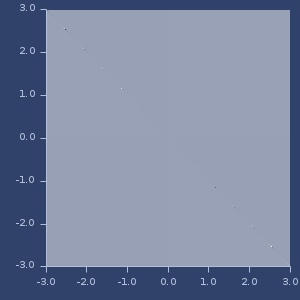
Plot of circular
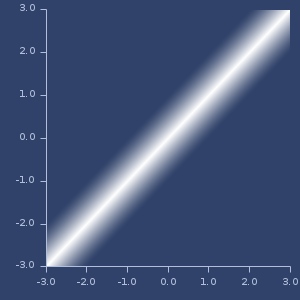
Plot of dirichlet
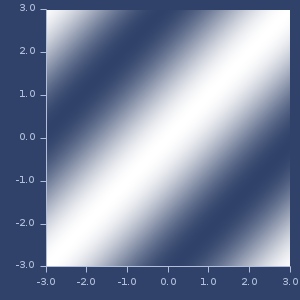
Plot of exponential
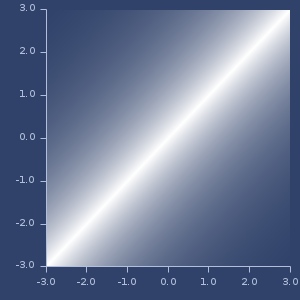
Plot of gaussian
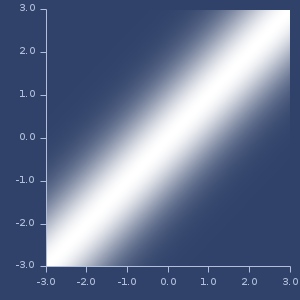
Plot of generalized-histogram
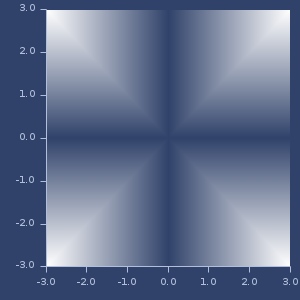
Plot of generalized-t-student
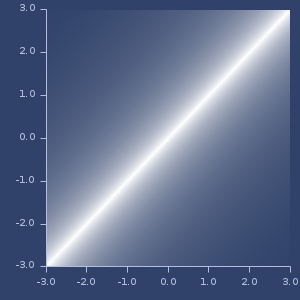
Plot of hellinger
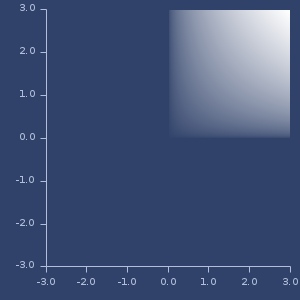
Plot of histogram
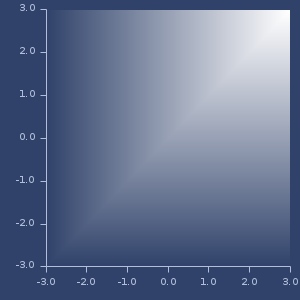
Plot of hyperbolic-secant
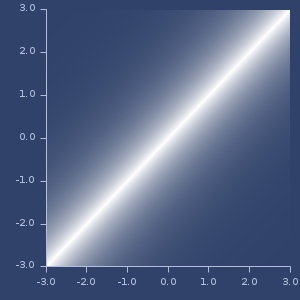
Plot of hyperbolic-tangent
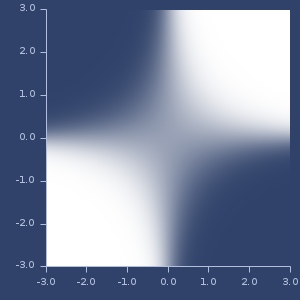
Plot of inverse-multiquadratic
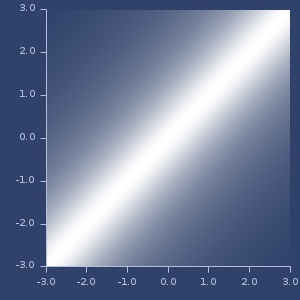
Plot of laplacian
Plot of linear
Plot of log
Plot of mattern-12
Plot of mattern-32
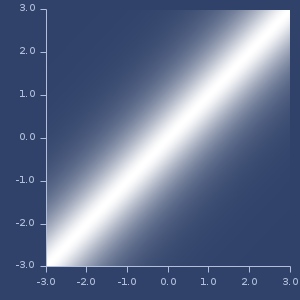
Plot of mattern-52
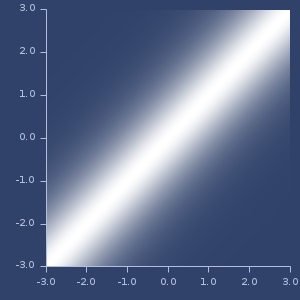
Plot of multiquadratic
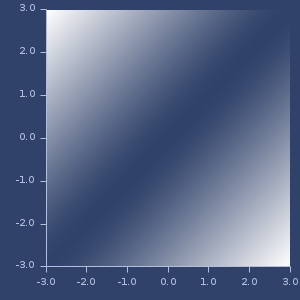
Plot of pearson
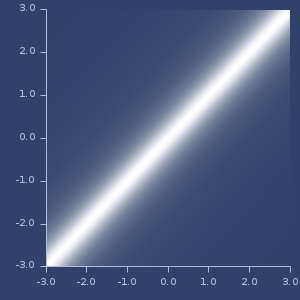
Plot of periodic
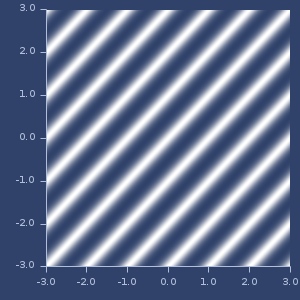
Plot of polynomial
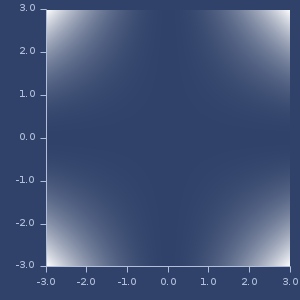
Plot of power
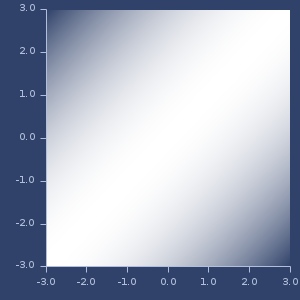
Plot of rational-quadratic
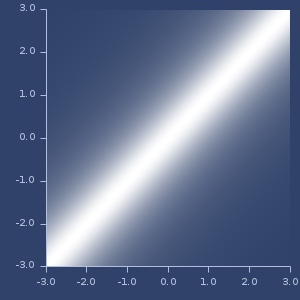
Plot of scalar-functions
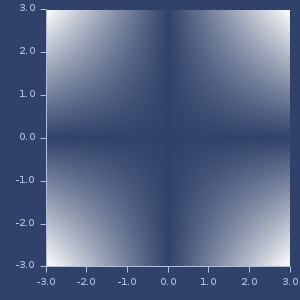
Plot of spherical
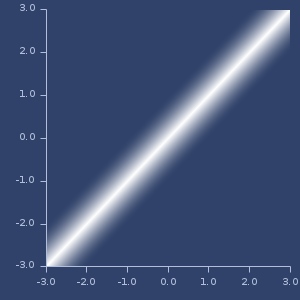
Plot of spline
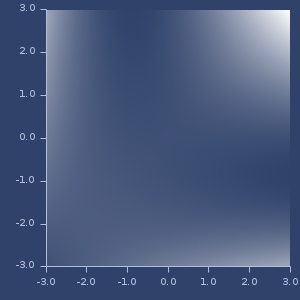
Plot of thin-plate
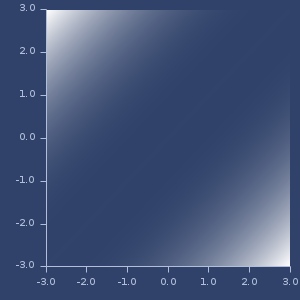
Plot of variance-function
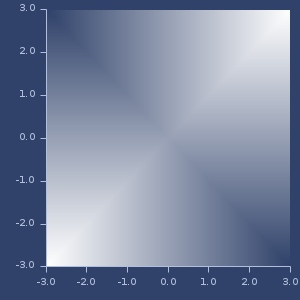
Plot of wave
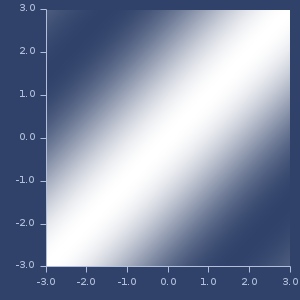
kernel->rbf
(kernel->rbf k)(kernel->rbf k center)Convert vector kernel to RBF kernel. center is fixed y vector (default contains EPSILON values).
Examples
Usage
(let [k (kernel :mattern-52) r (kernel->rbf k)] (r 0.234))
;;=> 0.9567485662415672kernel-density
multimethod
Create kernel density estimator.
Parameters:
- kernel name, see kernel-density-list.
- sequence of data values
- optional: bandwidth (by default, bandwidth is estimated using nrd method)
Examples
Usage
(let [k (kernel-density :epanechnikov (repeatedly 1000 rand))] (k 0.5))
;;=> 1.0512752150282882
(let [k (kernel-density :gaussian (repeatedly 1000 rand) 2)] (k 0.5))
;;=> 0.19742209649349005Plot of cauchy
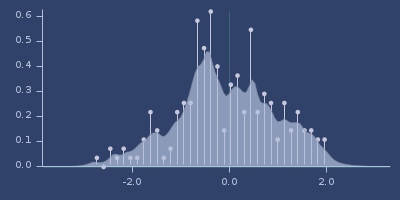
Plot of cosine
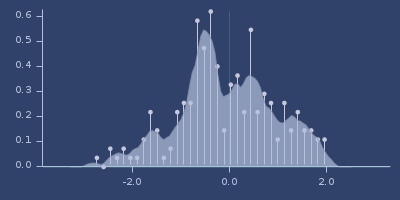
Plot of default
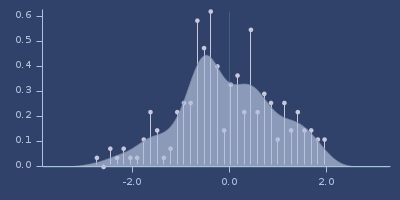
Plot of epanechnikov
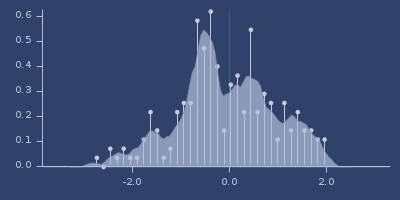
Plot of gaussian
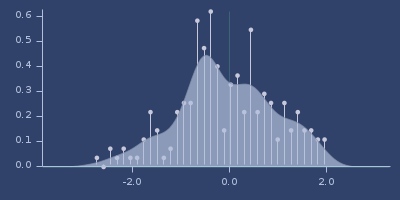
Plot of laplace
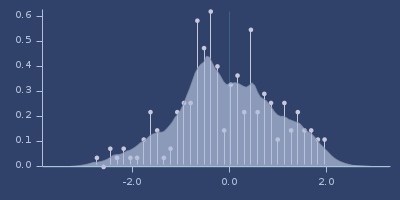
Plot of logistic
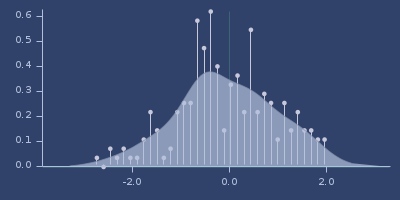
Plot of quartic
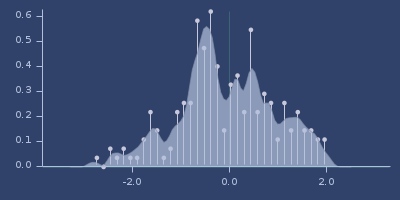
Plot of sigmoid
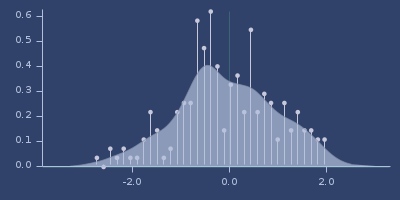
Plot of silverman
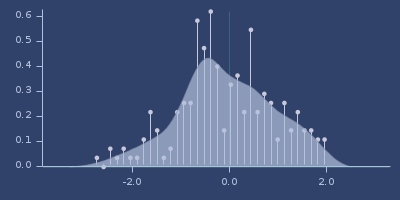
Plot of smile
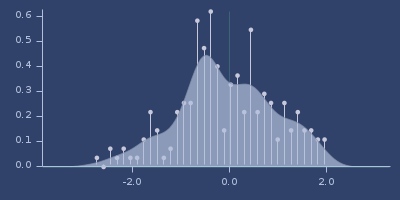
Plot of triangular
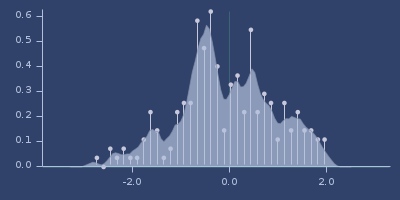
Plot of tricube
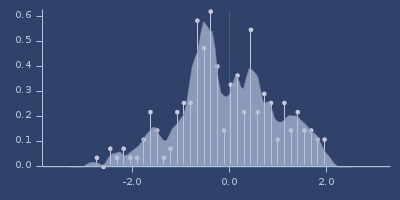
Plot of triweight
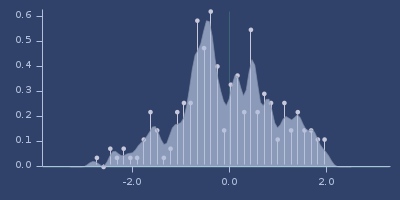
Plot of uniform
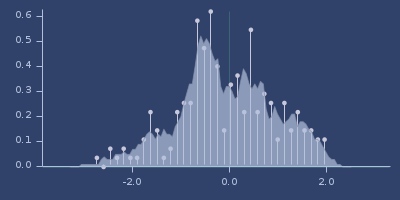
Plot of wigner
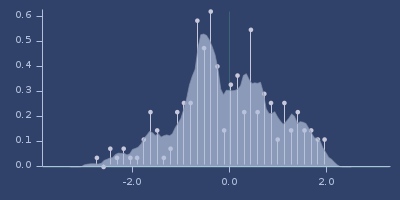
kernel-density-ci
(kernel-density-ci method data)(kernel-density-ci method data bandwidth)(kernel-density-ci method data bandwidth alpha)Create function which returns confidence intervals for given kde method.
Check 6.1.5 http://sfb649.wiwi.hu-berlin.de/fedc_homepage/xplore/tutorials/xlghtmlnode33.html
Parameters:
method- kernel namedata- sequence of data valuesbandwidthalpha- confidence level parameter
Returns three values: density, lower confidence, upper confidence
Examples
Usage
(let [k (kernel-density-ci :epanechnikov (repeatedly 1000 rand))]
(k 0.5))
;;=> [1.054111989255049 0.8775767959970229 1.2306471825130751]
(let [k (kernel-density-ci :gaussian (repeatedly 1000 rand) 2)] (k 0.5))
;;=> [0.19740451948239623 0.1870624090009602 0.20774662996383228]Kernel density with confidence intervals
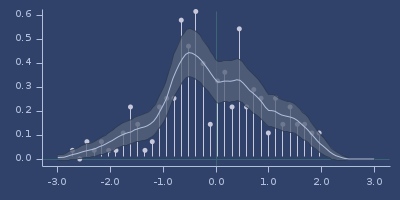
kernel-density-list
Examples
List of density kernels
kernel-density-list
;;=> (:cauchy :cosine
;;=> :default :epanechnikov
;;=> :gaussian :laplace
;;=> :logistic :quartic
;;=> :sigmoid :silverman
;;=> :smile :triangular
;;=> :tricube :triweight
;;=> :uniform :wigner)kernels-list
Examples
List of vector kernels
kernels-list
;;=> (:anova
;;=> :bessel
;;=> :cauchy :chi-square-cpd
;;=> :chi-square-pd :circular
;;=> :dirichlet :exponential
;;=> :gaussian :generalized-histogram
;;=> :generalized-t-student :hellinger
;;=> :histogram :hyperbolic-secant
;;=> :hyperbolic-tangent :inverse-multiquadratic
;;=> :laplacian :linear
;;=> :log :mattern-12
;;=> :mattern-32 :mattern-52
;;=> :multiquadratic :pearson
;;=> :periodic :polynomial
;;=> :power :rational-quadratic
;;=> :scalar-functions :spherical
;;=> :spline :thin-plate
;;=> :variance-function :wave)mult
(mult k1)(mult k1 k2)(mult k1 k2 k3)(mult k1 k2 k3 & r)Kernel wrapper. Multiply two or more kernels.
Examples
Usage
(let [k1 (kernel :laplacian)
k2 (kernel :periodic)
res (mult k1 k2)]
(res [1 2 3 4] [-1 2 3 5]))
;;=> 0.042910348739392076Product of two kernels
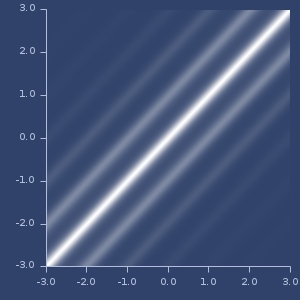
rbf
multimethod
RBF kernel creator. RBF is double->double function.
Parameters:
All kernels accept scale parameter (as last parameter).
Following kernels also accept beta: :multiquadratic, :inverse-multiquadratic, :truncated-power, :radial-powers and :thin-plate.
Examples
Usage
(let [k (rbf :gaussian)] (k 1))
;;=> 0.36787944117144233
(let [k (rbf :gaussian 0.5)] (k 1))
;;=> 0.01831563888873418Thin-plate RBF with
beta=2andscale=1
(let [k (rbf :thin-plate 2.0 1.0)] (k 0.5))
;;=> -0.04332169878499659Plot of above RBF
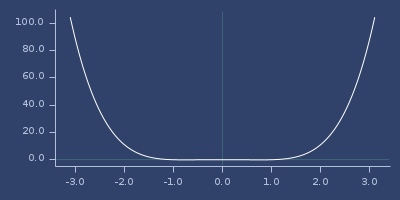
Plot of gaussian
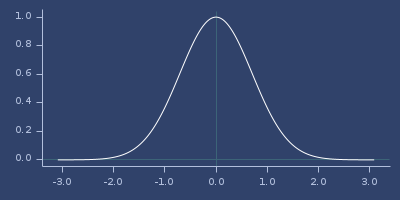
Plot of gaussians-laguerre-11
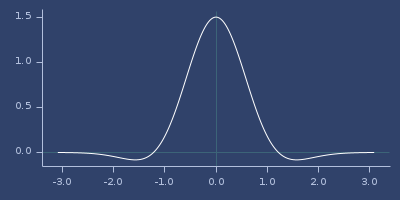
Plot of gaussians-laguerre-12
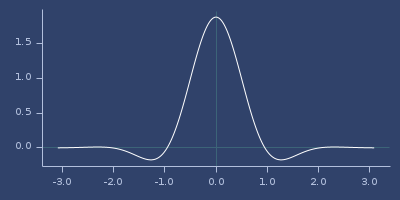
Plot of gaussians-laguerre-21
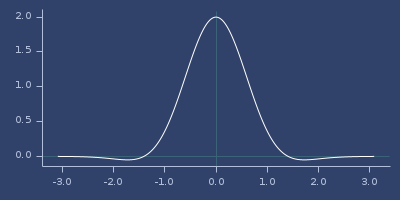
Plot of gaussians-laguerre-22
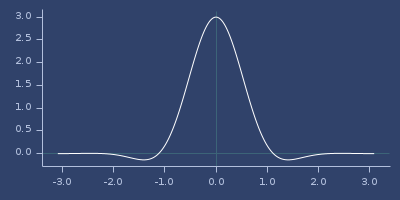
Plot of inverse-multiquadratic
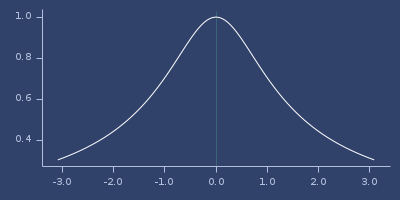
Plot of linear
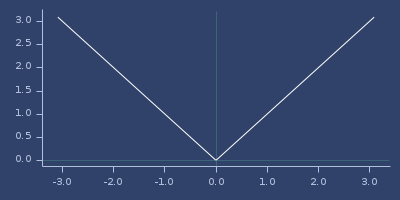
Plot of mattern-c0
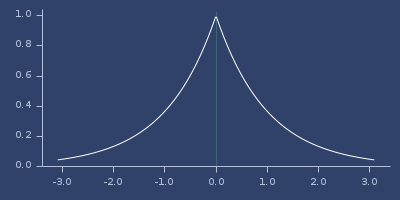
Plot of mattern-c2
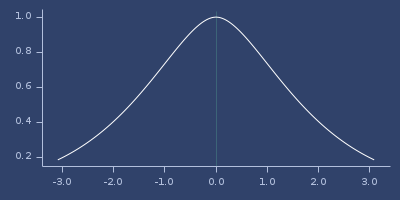
Plot of mattern-c4
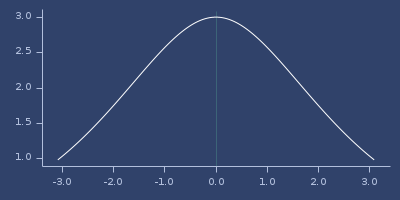
Plot of multiquadratic
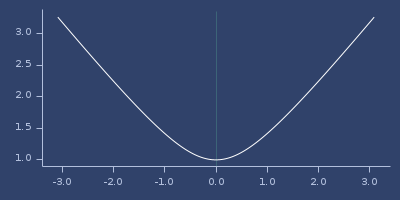
Plot of poisson-2
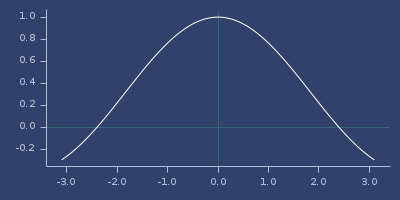
Plot of poisson-3
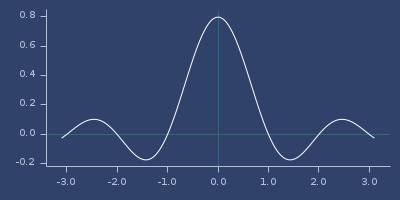
Plot of poisson-4
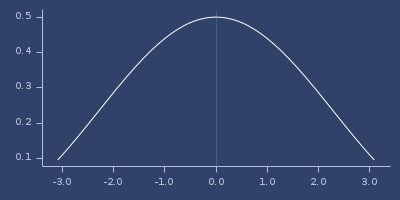
Plot of radial-powers
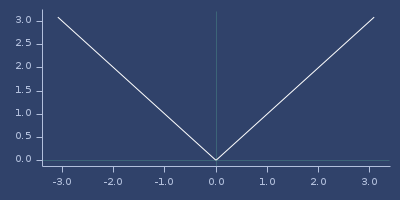
Plot of thin-plate
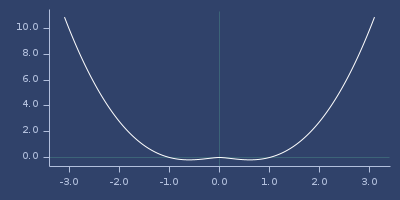
Plot of truncated-power
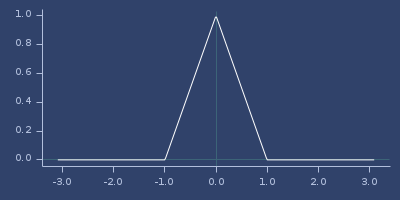
Plot of wendland-10
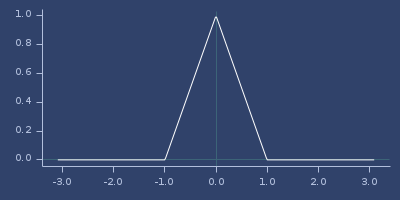
Plot of wendland-20
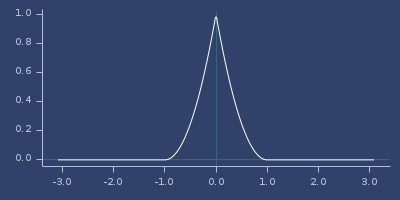
Plot of wendland-21
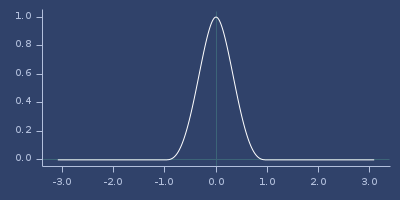
Plot of wendland-30
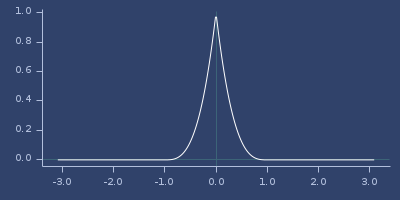
Plot of wendland-31
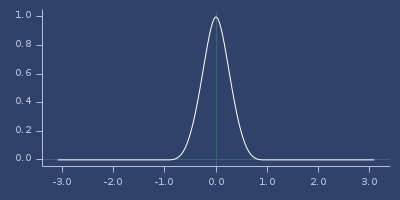
Plot of wendland-32
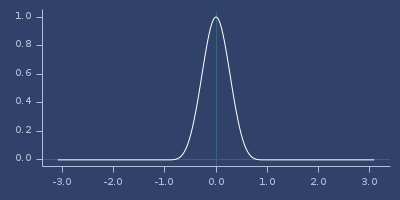
Plot of wendland-41
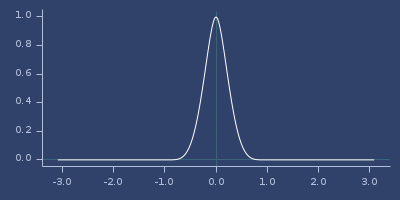
Plot of wendland-42
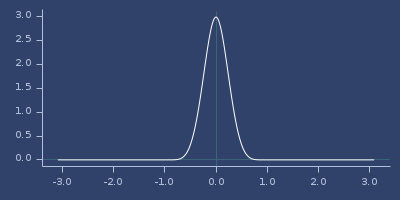
Plot of wendland-52
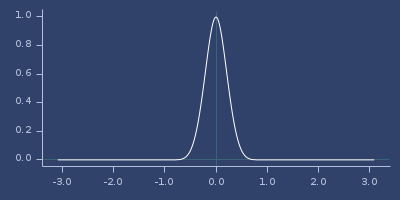
Plot of wendland-53
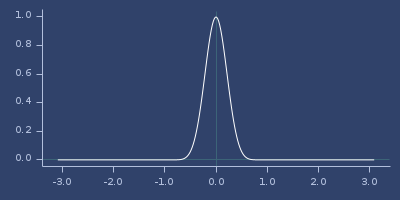
Plot of whittaker-02
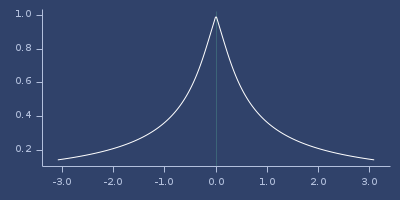
Plot of whittaker-03
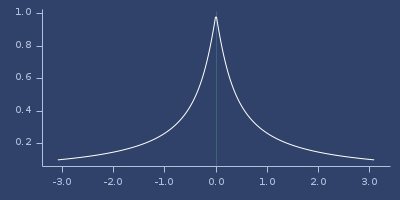
Plot of whittaker-12
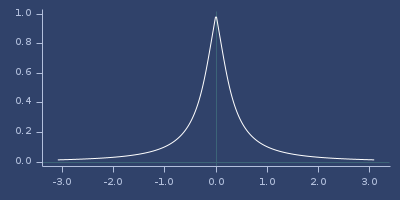
Plot of whittaker-13
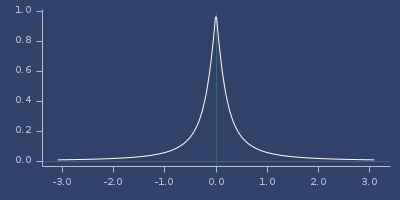
Plot of wu-00
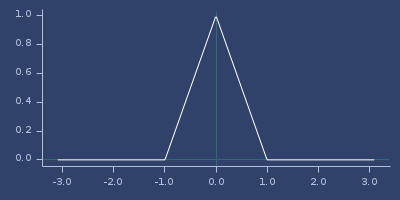
Plot of wu-10
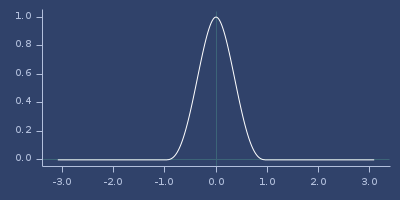
Plot of wu-11
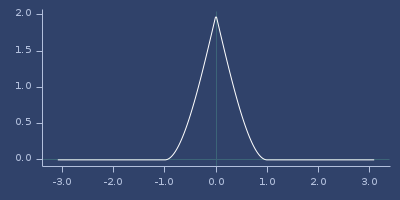
Plot of wu-20
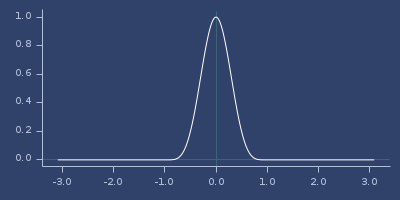
Plot of wu-21
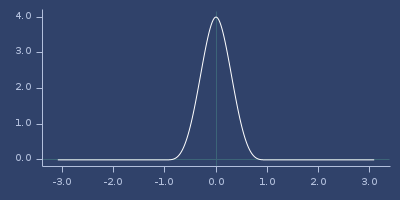
Plot of wu-22
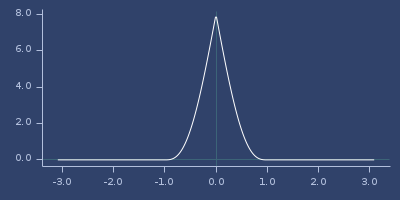
Plot of wu-30
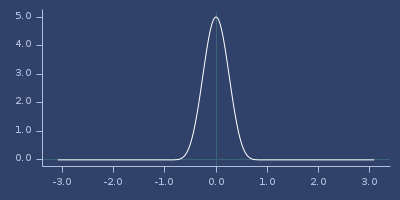
Plot of wu-31
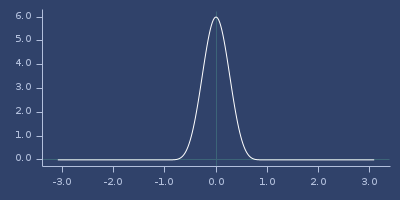
Plot of wu-32
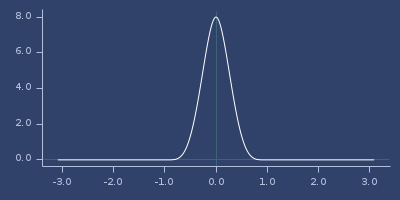
Plot of wu-33
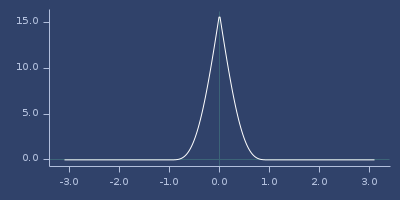
rbf->kernel
(rbf->kernel rbf-kernel)(rbf->kernel rbf-kernel distance)Treat RBF kernel as vector kernel using distance function (default euclidean.
Examples
Usage
(let [r (rbf :mattern-c4) k (rbf->kernel r)] (k [1 2 3 4] [-1 2 3 5]))
;;=> 1.5719823264954609rbf-list
Examples
List of RBF kernels
rbf-list
;;=> (:gaussian
;;=> :gaussians-laguerre-11 :gaussians-laguerre-12
;;=> :gaussians-laguerre-21 :gaussians-laguerre-22
;;=> :inverse-multiquadratic :linear
;;=> :mattern-c0 :mattern-c2
;;=> :mattern-c4 :multiquadratic
;;=> :poisson-2 :poisson-3
;;=> :poisson-4 :radial-powers
;;=> :thin-plate :truncated-power
;;=> :wendland-10 :wendland-20
;;=> :wendland-21 :wendland-30
;;=> :wendland-31 :wendland-32
;;=> :wendland-41 :wendland-42
;;=> :wendland-52 :wendland-53
;;=> :whittaker-02 :whittaker-03
;;=> :whittaker-12 :whittaker-13
;;=> :wu-00 :wu-10
;;=> :wu-11 :wu-20
;;=> :wu-21 :wu-22
;;=> :wu-30 :wu-31
;;=> :wu-32 :wu-33)scale
(scale k scale)Kernel wrapper. Scale kernel result.
Examples
Usage
(let [k (kernel :laplacian)
sk (scale k 2.0)]
{:kernel (k [1 2 3 4] [-1 2 3 5]),
:scaled-kernel (sk [1 2 3 4] [-1 2 3 5])})
;;=> {:kernel 0.10687792566038574, :scaled-kernel 0.2137558513207715}smile-mercer
(smile-mercer k)Create Smile Mercer Kernel object
Used to pass to Smile constructors/functions.
Examples
Usage
(smile-mercer (kernel :mattern-52))
;;=> fastmath.kernel$smile_mercer$reify__21471@7208c8d8smile-rbf
(smile-rbf rbf-fn)Create RBF Smile object.
Used to pass to Smile constructors/functions.
Examples
Usage
(smile-rbf (rbf :mattern-c2))
;;=> fastmath.kernel$smile_rbf$reify__21209@692ef762wadd
(wadd kernels)(wadd weights kernels)Kernel wrapper. Add kernels (weighted).
Examples
Usage
(let [k1 (kernel :laplacian)
k2 (kernel :periodic)
res (wadd [k1 k2])]
(res [1 2 3 4] [-1 2 3 5]))
;;=> 0.5083672741320578Weighted sum
(let [k1 (kernel :laplacian)
k2 (kernel :periodic)
res (wadd [0.2 0.8] [k1 k2])]
(res [1 2 3 4] [-1 2 3 5]))
;;=> 0.3425670639094149Weighted sum of two kernels